1. 振幅
这个看波形就好理解,既然每个点都在各自的位置上振动,那么一定是在一定范围内的,不可能离开原来的位置再也回不去,对吧?所以各点离开原来位置的最远距离就是振动的最大幅度,简称为振幅。在波形振动图上,振幅通常指的是压力值,因为图形描述的是“压力随时间变化关系”,即横坐标轴(X)为时间轴,纵坐标轴(Y)为压力值。
2. 周期
我们从波形上可以看到波向远处传播时,在某一时刻的静态波形有一定规律的重复,我们可以找在相同位置的点,最容易找的是位于坐标轴上的点,选取离得最近的两点且两点间所包含的区间波形与后续每隔两点的波形完全相同,这两点间就是一个周期,对应横坐标(时间轴)的两个刻度差就是时间差,所以周期就是相同波形重复出现的最短时间,单位就是时间单位 – 分钟(mins.)、秒(s)、毫秒(ms)等。
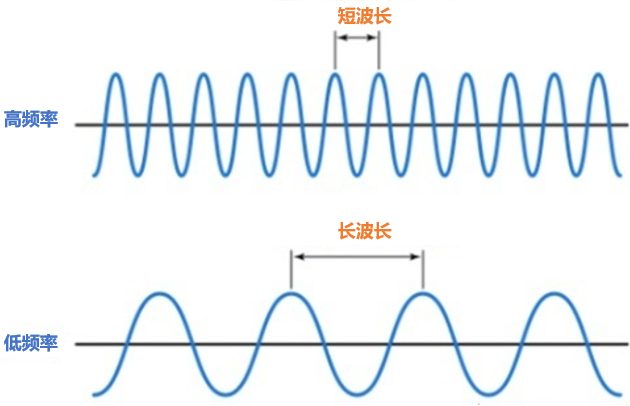
3. 频率
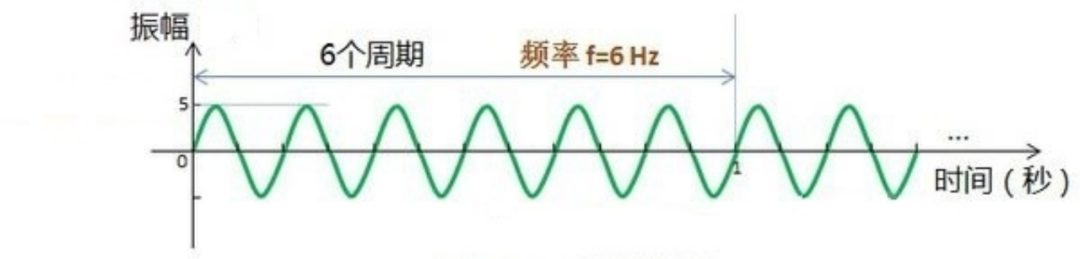
教科书上通常说频率是周期的倒数 ,公式通常都是枯燥无味的!其实也好理解,上面说“周期是规律重复出现的最短时间”,频率其实就是在规定的时间段内出现多少个周期,而这个“规定时间”就规定为1秒,所以1秒内出现多少个周期,就是频率,频率单位规定使用“赫兹”(Hz)。当然你也可以这样直白得描述“每分(或秒或毫秒)多少个波”,当然规范的国际度量单位赫兹永远指的是1秒内多少个周期。
4. 相位
多多觉得“相位”是最难理解的小古怪。对一个因质点振动且向远处传播的机械波形,我们可能希望知道在某一时刻,各个质点在波形中所处的相对位置关系。一般都是各点相对于振源(第一个开始振动的点),通常是坐标原点。那么应该怎么来表达这种相对关系呢?
请看下面动图,我们不难发现各质点在做直线往复运动所产生的传播波形,可看成“一个质点”在做一个圆周运动。
What? Emmm。。。。。。
好像哪里有点不对劲。。。。。。
一定会有杠精跳出来说“多多上次说过,波在传播过程中,各个质点一直在“原地”来回振动,并不会沿波的传播方向往前跑~这显然不是一个点在运动”。是的,没毛病!不要被动图迷惑了,其实这只是为了便于理解下一步的知识点,虚构出来的圆周运动而已。它是这么虚构出来的,动图上做圆周运动的点,其实代表了在波向前传播过程中不同时刻的各个质点,子曰:“它不是一个人在战斗,是很多人在战斗”。
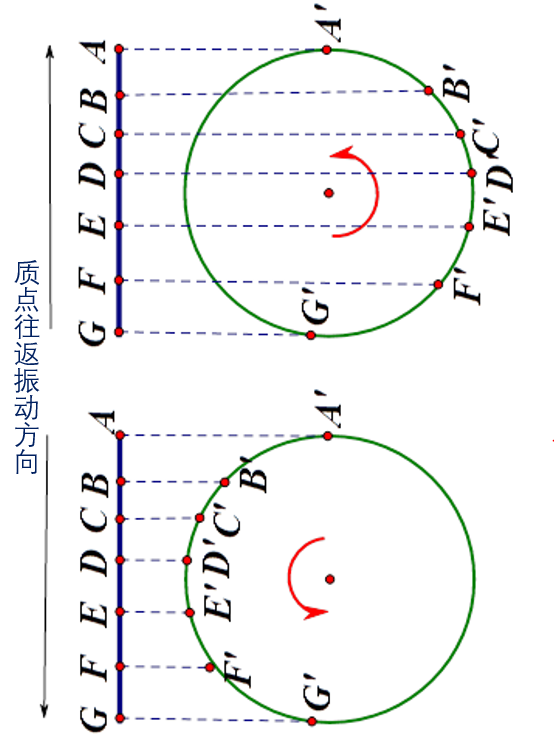
换句话讲,如果把波形上在某一时刻,一个周期波形内位于不同位置的质点放在一起,就会拼成一个圆。就像下面这样(不好意思,取得点少了一点,不够缜密哈,请自行脑补加密,然后圆就出现了)。
多多已经使出洪荒之力,要还是不明白,多多只能躲到墙角里哽咽一下。。。。。。然后继续。。。。。。所以,要描述某一点相对于振源(原点)的关系,就是看某一点在这个“虚构”出来的圆周上对应点与起始点的关系。我们可以看下具体怎么表示,
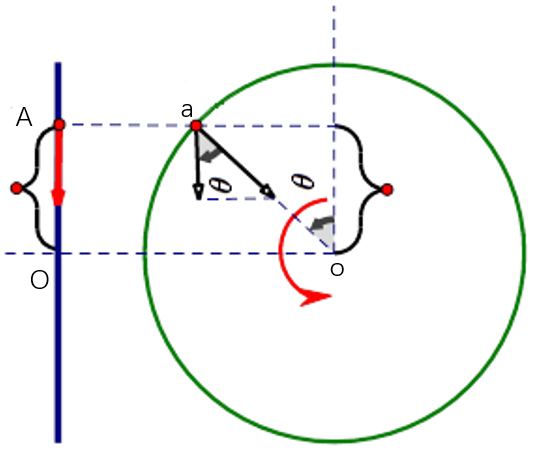
图中A点要返回O点(原点,即最初起振位置),则相对于O点的位置关系相当于在虚构的圆周运动中,A的投影点a运动方向向下(运动方向是客观存在不能变)与a离开o的距离连线(振幅也不能变)之间的夹角θ,这就是传说中的相位角或相位。
因为角度是60进位制,在数学物理计算时相对麻烦(总要单位换算~太烦了),因此通常用弧度来描述。1弧度就是一段等于圆半径长的圆弧所对应的圆心角,习惯上在写相位值时略去单位“弧度”(或rad),表示为一个实数,如:2π/3 (我们知道一个π就是180°)。
所以,我们很容易就能理解波峰和波谷就是90°(π/4)和270°(3π/4)当然如果不需要进行数学物理的量化表达时,我们只要知道相位是正或负(坐标轴X的上方为正,下方为负)即可,就是通常说的正压相、负压相。
5. 波长
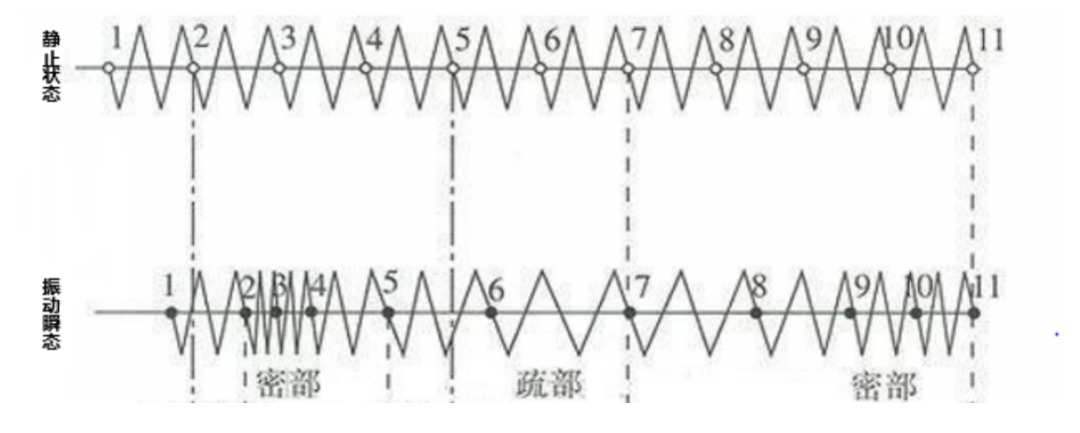
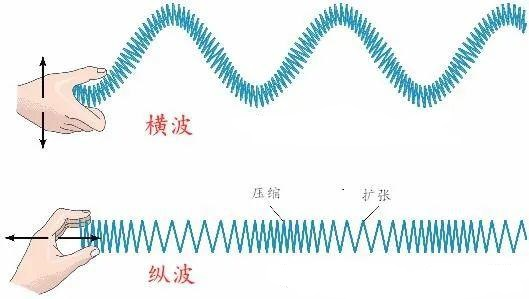
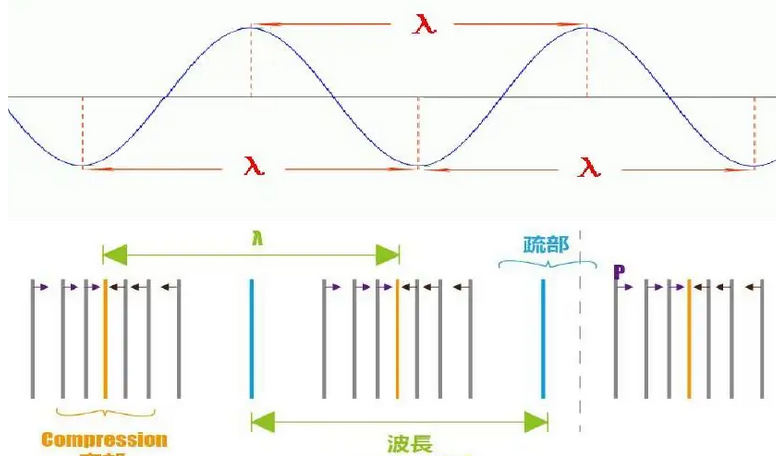
跟我们每个人都有身高类似,每个波也有自己的“身高”,叫做波长。只不过,人的身高是从头到脚作为一个完整的整体,而波是周期性重复,总是从头到脚的循环,也就是如“相位”中描述的,完成一个完整的虚拟圆,即总是相差360°(2π)。因此,波形图上任意两个相差2π的点之间,就是波的身高,即“波长”,通常用希腊字母λ,/'læmdə/表示。跟我们人身高有高矮一样,不同的波也有长短。通常我们讨论是横波的波长,而纵波的波长则是相差一个相邻的疏部或密部,也就是相差2π(一个周期)。
6. 波速
对于波长,我们还可以换一个角度理解:波长其实就是波在一个周期内所跑过的距离。所以想知道波跑得快慢,也就是速度,显然用跑过的距离(波长)除以时间(周期)就可以得到速度,这个速度就是波的移动速度,称为“波速”,通常用c(或ν/nju:/)。由此,我们知道波长、波速和周期(或频率)间的关系,即:ν= λ/T,而根据周期和频率互为倒数关系T=1/f,我们又可以得到波长和频率的关系:ν=λ*f。
以上,就是用于描述机械波的常用主要物理特征参数,理解这些常见物理参数是深入学习了解声波的必要基础。
本文转载自多尼尔高研院
图片来源于专业网站,侵权删